Prime Numbers
Whilst bored one day I watch a youtube video about prime number spirals.
Being a programmer of sorts I decided to knock up a bit of code to draw these myself. I started with just replicating prime spirals.
You do this by plotting the prime numbers in ever wider circles.
So we’d take the first prime (1) and we’d draw it somewhere in a circle which was 1 unit away from the centre.
Where on that circle? Well a circle is 2 PI radians around (about 6.3), so if we were plotting the number 1, it’d be about 1/6th around the circle (sort of 2 o’clockish).
The next prime (2) we draw in a circle ‘2’ units from the centre (because it’s the second prime number, so we draw it about 1/3rd around the circle.
And so on.. the prime number 5, we draw in the 4th shell (it’s the 4th prime number) and it’s at about 10 o’clock on the circle (2 pi / 5) etc.
Because all primes are odd numbers (except 2) they’ll all end in a 1,3,7 or 9, so we can colour the dots accordingly.
This is what it look like at varying levels of zoom.


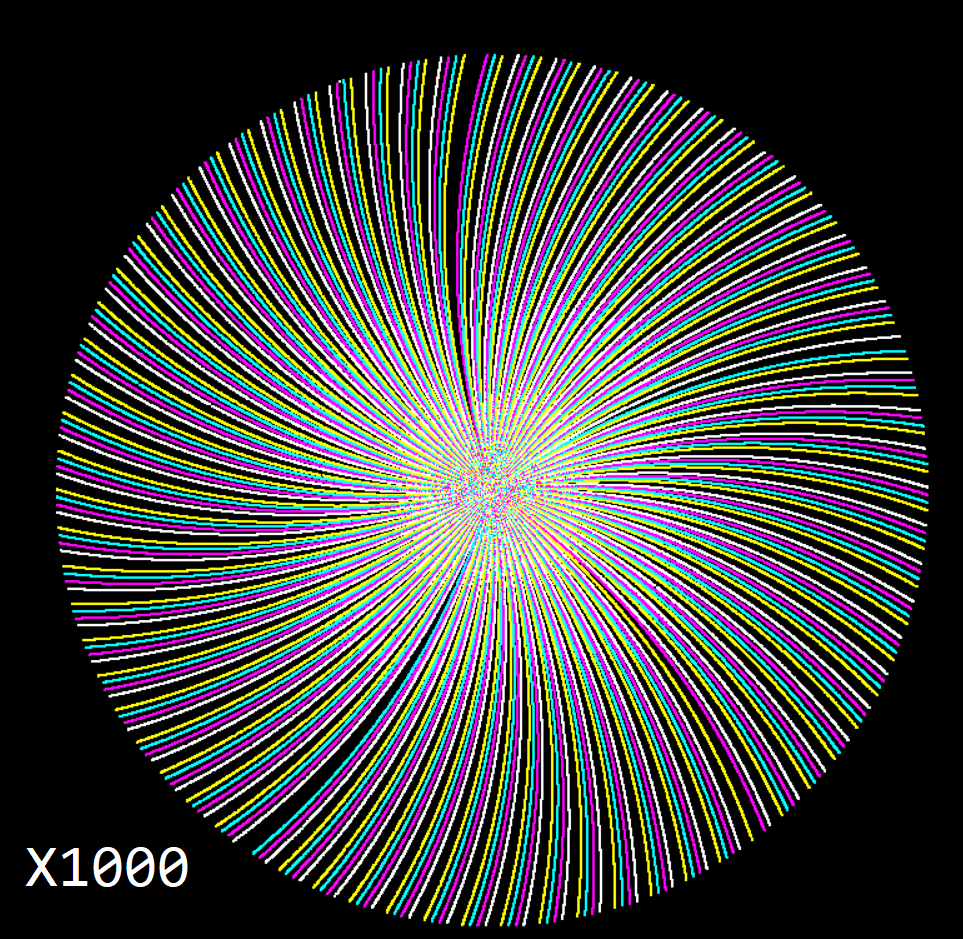
My big idea was this.. What’s the point in using 2 PI radians. Why not make a circle ’10’ around? What would happen if we did that? I mean, we count in base 10. In an ideal world I’ll see straight lines, giving me a chance to be able to create some sort of equation to predict prime numbers. And if I can predict prime numbers I’m going to be so rich I’ll be able to build a house out of £20 notes. This is what happens when you make a circle ’10’ units around instead of ‘2PI’ units around :
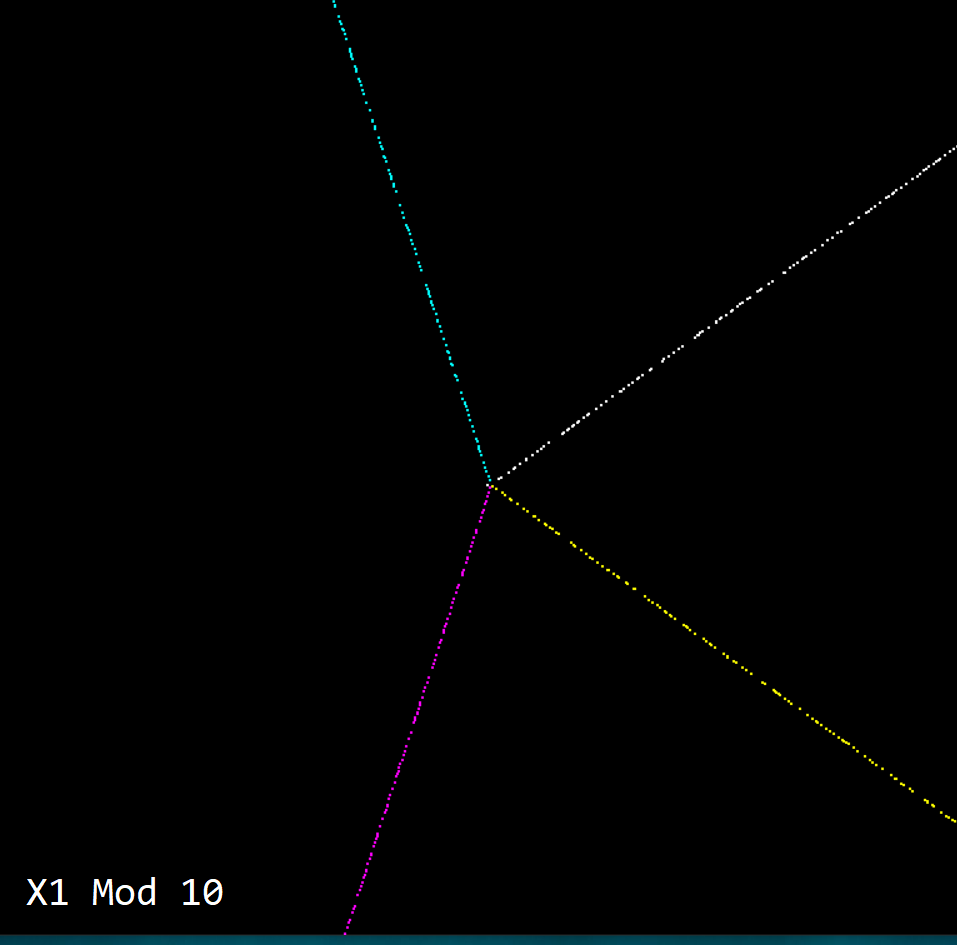
OMG! I’m RICH!!!
So I sat there, staring at the screen for a few minutes thinking, it’s very unlikely that I have discovered something that Gauss, Fermat or Euler have missed, so what’s going on?
What happens if I make a circle some other arbitrary number around, let’s try 7.
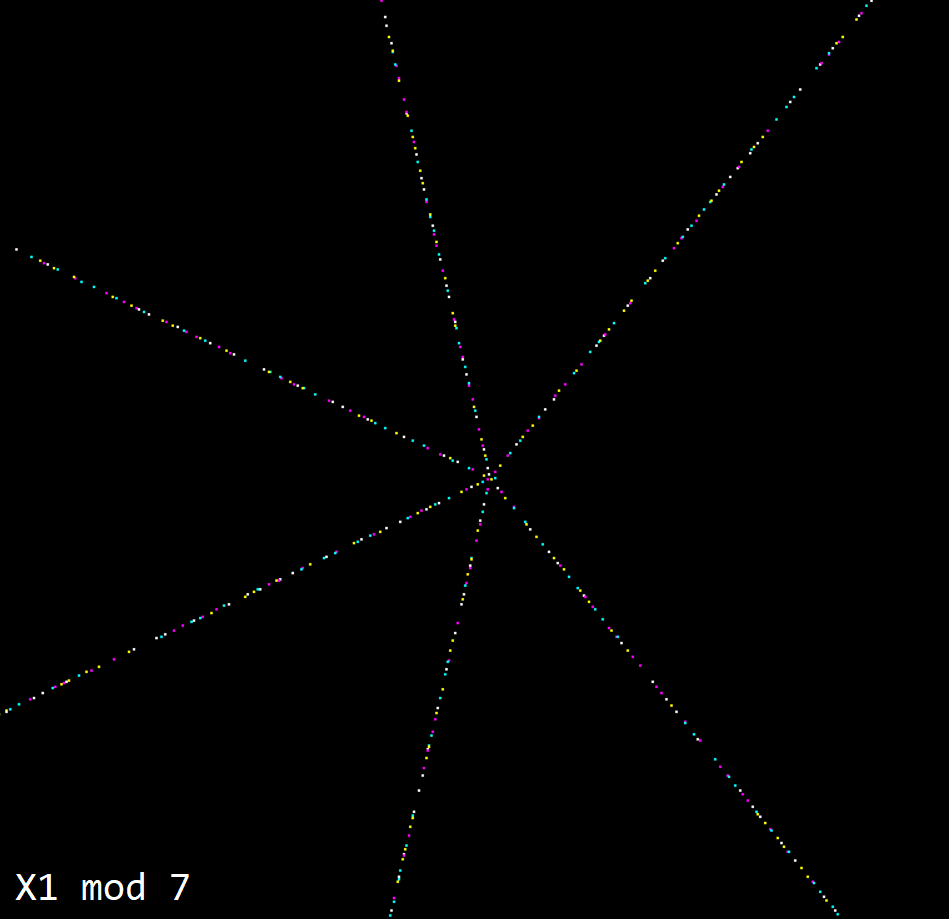
No, this is a mess in comparison. The colours are all mixed, and the ideal number of ‘rays’ is 4. One for each possible last digit (1,3,7,9).
What’s the lowest number I can make the circle and still get 4 clean rays?
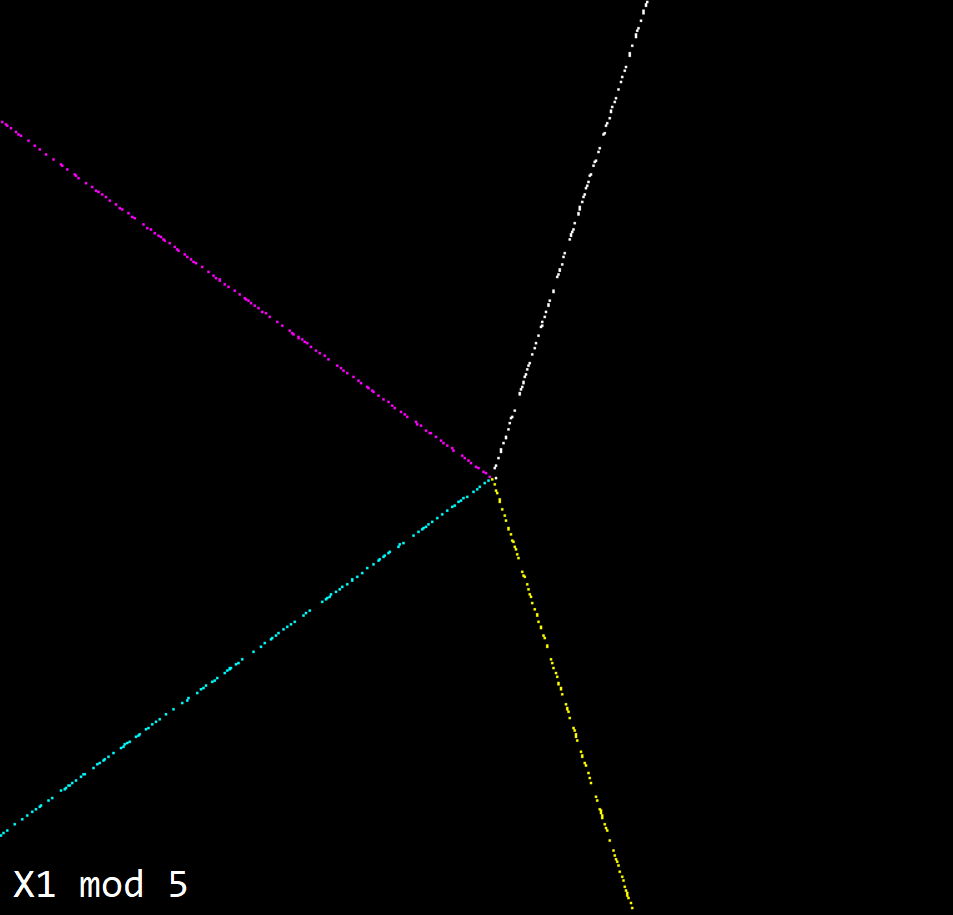
Ok, so it turns out a circle of 5 units around gives me 4 clean rays. Large numbers give me too many rays, or rays with mixed colours. What is it about 5 that’s special? Well, 5 is the most interesting number. If I can be bothered I’ll do a post about Roger Penrose and 5 fold symetry and how it links to the Golden Ratio etc.
But it turns out 5 is not interesting per se.
What’s going on here is that all the primes effectively get ‘mod 5ed’.
That’s why we get 4 clean rays. But hey, we’re a step closer aren’t we?
Now we know that all prime numbers can be drawn on lines with polar angle (2pi / 5) * ending (about 1.2566371 radians for numbers ending in a 1 etc.).
So we can calculate the angle in polar coordinates.
If we can also calculate the radius, we can use simple Pythagorean geometry to predict prime numbers, and we’ll be immortal!.
How do we calculate the radius? Well.. this is where it gets complicated 🙂
Notice that the lines in the mod pictures above have random gaps in them. I need to find out if there is any pattern to those gaps.
NOTE : Of course.. this is the whole point isn’t it!
What if, instead of plotting the prime numbers themselves, I plot the gap between primes. So we take the first 5 primes 1,2,3,5,7, the gaps are 1,1,2,2 (hey, there’s a pattern! He says with his tongue in his cheek.)




So what I did here was divide the prime number by the previous prime, then multiply by a large number to get numbers in the range of 1 to 2 (or 10 to 20 etc.) ie 29/23=1.26086956522 * 10 = 12.6.. etc.
We know we can do this because of Erdos’s proof of Betrand’s postulate (lolz :))
This gives us a way of getting a ‘gap’ which doesn’t grow as the size of the primes grow. I’m not going to go into much detail about the results except to say you should click on the X1000 photo and know that we live in the matrix.
It seems that at large scale, the gap between primes does seem to give us some sort of pattern. But I’m not sure if these ‘artifacts’ are related to how I’m doing the calculations or if they really exist.
At x10000 we can see 39 rays. That is, the gaps between primes appear to fall into roughly 40 discrete sizes. Have I discovered something, or is this more stating the obvious?
To be continued.. possibly. When I’ve understood the 6n + 1 thing..